0000(112) (121) (211)
0001
0010
0011(033) (303) (330)
0100
0101
0110
0111
1000
1001
1010
1011
1100(003)(030) (300)
1101
1110
1111(122) (212) (221)
There is only one way to move,
But three ways to stand still.
-- Book of Trigrams
As I alluded to earlier, while this definition of the hierarchy is consistent with the old, traditional scheme, it clearly points out some "major weirdness" going on with the trigrams. This can easily be seen to be a consequence of the fundamental mathematical principle known as "the pidgeonhole principle": if you have m letters and n mail slots, where m is greater than n, then some mail slot is guaranteed to have more than one letter. We saw this already with the 8 traditional trigrams which are paired up with only 4 emblematic lines (and their journeys): some of the trigrams have to have the same journey. This is why all the sons have the same behavior in the hexagram, as do all the daughters. In TL(2), 512 hypertrigrams are chasing only 16 journeys, so the crowding is even worse. As we go up the hierarchy, 23n hypertrigrams are being stuffed in only 22n slots for journeys. A few minutes with a calculator should convince you that some of these mail slots are quite stuffed indeed.
The situation for TL(1) is summarized in Table 1. The tedious details of the situation for TL(2) are listed in Table 2, below. While non-mathematicians may not appreciate the beauty of the patterns in this table, it fully captivated me for over a week before surrendering its messages. It shows which hypertrigrams have which journeys, so any TLs in the same row of this table have the same behavior and are "equivalent" in some sense. More formally,
Def: If f, g are both in TL(n), then f is equivalent to g or f~g if and only if Hn(f) = Hn(g). (Remember, Hn calculates the journey of a TL.)
There is an abbreviation used throughout Table 2 to make it shorter and more understandable. As we saw earlier, it doesn't matter which trigrams are on the lower level of the TL so much as whether they are mother=0, son=1, daughter=2 or father=3. All the sons lead to the same results, as do daughters. Thus, a sequence like ( 000 110 010 ) can be shortened to (021), since we don't need to know which daughter or son was in the original sequence. This abbreviation makes the journey calculations bearable, even with pen and paper. (I would not even think of doing the equivalent calculations for TL(3) without a computer!)
| Journey | Member Hypertrigrams | Number |
|---|---|---|
| 0000 |
(013) (031) (103) (130) (301) (310) (112) (121) (211) |
99 |
| 0001 |
(233) (323) (332) | 9 |
| 0010 |
(011) (101) (110) | 27 |
| 0011 |
(123) (132) (231) (213) (312) (321) (033) (303) (330) |
57 |
| 0100 |
(002) (020) (200) | 9 |
| 0101 |
(222) | 27 |
| 0110 |
(000) | 1 |
| 0111 |
(022) (202) (220) | 27 |
| 1000 |
(113) (131) (311) | 27 |
| 1001 |
(333) | 1 |
| 1010 |
(111) | 27 |
| 1011 |
(133) (313) (331) | 9 |
| 1100 |
(012) (021) (102) (120) (201) (210) (003)(030) (300) |
57 |
| 1101 |
(223) (232) (322) | 27 |
| 1110 |
(001) (010) (100) | 9 |
| 1111 |
(023) (032) (203) (230) (302) (320) (122) (212) (221) |
99 |
As can be easily seen, these equivalence classes vary in size quite a bit. While all yin lines (000) and all yang lines (333) are the sole members of their classes, the largest classes (corresponding to static yin and static yang) are loaded with 99 TL's each. Since each TL is just as likely as the next one to be cast when the oracle is consulted (more or less), that means static lines are still the most probable lines in a hexagram. In fact, the equivalents of the 4 emblematic lines in TL(2) are roughly 60% of the total mix. The other 40% accounts for non-standard forms of movement.
Among the many fascinating symmetries in this table, it appears that if you take any TL (call it f) and make a new TL g by scrambling or rearranging the numbers in the sequence, then f and g are equivalent. Look in the first row, for instance. The trio of (112), (121) and (211), consisting of 2 static yangs and 1 static yin, exemplifies the old wisdom that all the daughters look the same. But the sextet of (013) through (310) shows all 6 possible sequences of 0, 1 and 3. This is a red flag for mathematicians, as it shows the workings of a well-known algebraic system, the permutation group of order 3 or S(3). S(3) is the group describing all the ways there are to rotate or flip a triangle around. It can't change yin lines to yang ones or vice versa, but it can move them around in any order. It can change a first son to a second or third son, for instance, but it can't change a son into a daughter. In short, these equivalence classes are simply collections of TL's that are "basically the same, but in a different order", as it were. And we have our first big clue: think triangles.
(Incidentally, you can flip things around at the lower level trigrams as well as the upper trigram and still not affect the journey in the end.)
The two functions used to define the interpretation functions, odd() and fewer(), are completely insensitive to order considerations. In fact, the original algorithm of the yarrow stick method is based on adding the 3 yin=2/yang=3 lines in a trigram and interpretting the results based on the sum (between 6 to 9). Addition is a commutative operation, a fancy term meaning it ignores order as well. So it appears all the h[n, j]'s are adept at picking out whether two TL's are equivalent, but are perfectly blind as to which one is which.
This is the reason why it appears a basic trigram (from TL(1)) has 3 lines, but only 2 bits of information. In fact, when you do the calculations precisely (using the information formula developed by Claude Shannon), a trigram is reduced to an emblematic line in the hexagram that contains only 1.82 bits, about .6 bits per line of the trigram. Where did the remaining 1.18 bits go to? That left over information is simply the order data that was filtered out of the trigram by H1 when it was reduced to an emblematic line. If you calculate how much data it takes to answer the question "If this is a son or daughter trigram, is it the first, second or third?", the answer comes to exactly 1.18 bits. Added to the 1.82 bits of non-order related information, the sum is 3 -- all bits are present and accounted for.
With higher order hypertrigrams, the amount of "lost data" is even more extreme. The percentage of information in a TL of order n that is devoted to specifying the journey is always somewhat less than (2/3)n. For order 2, it's about 44%, less than 20% for order 4, and less than 1% by order 12 (not that you'd ever want to use TL(12) in practice for actual divination purposes!). More and more of the information content of these TLs is locked up in the order information, making fewer order-free bits available for defining the journey. An incredible amount of data (not to mention effort to cast all those yarrow sticks) is simply thrown away, due to the way the old masters chose to interpret trigrams.
There's a new and provocative phenomenon that first appears with the second order TL's that wasn't present with the traditional 8 trigrams. I refer to this effect as "inner motion", the appearance of moving lines deep within the TL that "cancel out", leaving the TL as a whole perfectly static. It's similar to a person lying perfectly still in bed at night, while at a cellular level, all sorts of commotion is going on.
A good example is one we've already looked at, g = (111 001 000) = (310). The first and last sub-trigrams are both moving lines, but the upper level trigram only moves from one daughter to another. As a consequence, g is constantly yin at every step of its journey. Because the two moving lines are moving in opposite directions, they cancel each other out. So even though there is motion within, g is calm on the surface where it really counts when consulting the oracle.
Most examples of inner moving lines, however, also result in outer motion. Some of the resulting journeys for such figures can get quite complicated.
I've long attempted to find some kind of fractal representation of hypertrigrams that did justice to the "trigrams all the way down" aphorism. With the clue from S(3) to "think triangles", a new way of drawing TL's came to mind. Not only is it fractal, displaying the inner structure of a TL in an obvious way, but it makes the previous computations of Hn(g), apparently so difficult and obscure when expressed in typical math notation, a breeze. This is a scheme so simple, it could be taught to any initiate programmer in the Oracle Temple.
For convenience in this new "triangular calligraphy", yin lines will be represented by a blue square and yang lines by red squares (see Figure 2), though other notations are also possible. Instead of drawing a trigram as 3 lines stacked on top of each other, we will arrange the 3 colored squares in a triangle. Although the order of these squares within the enclosing triangle is perfectly arbitrary, for definiteness we will use the order in Figure 2b, namely the lowest line 0 (the earth position) is on top, the middle line 1 (human position) is in the lower right, and the upper line 2 (the heaven position) is in the lower left. Figure 2c thus shows the new representation of the 8 basic trigrams, that is, TL(1). Figure 2d shows the 2 typical members of TL(2) we used as examples previously, namely (111 010 011) and (111 001 000). Notice the sub-trigrams are arranged in the same order as specified in 2b.
Figure 2. Triangular Calligraphy for Hypertrigrams.
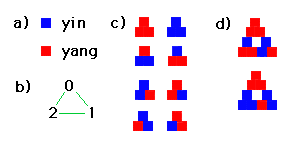
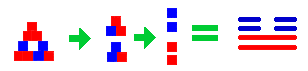
The nice thing about this new calligraphy is that it takes care of all the tedious bookkeeping associated with journey calculations automatically. Figure 3 shows the same journey calculation as did Figure 1, but using the new notation. At each step of the computation, a low level triangle is replaced by a single square in a new upper figure (the "before" picture) and a single square in a new lower figure ("after"). For instance, the low level triangle in position 0 is (111), moving yang. Thus it contributes a single yang square in position 0 of the upper triangle (it starts yang), and a single yin square in position 0 of the lower triangle (but it moves to yin). The triangle in position 1 is (010) or static yang, which contributes a yang square in position 1 of the new triangles. The triangle in position 2 is (011) or static yin, which generates 2 yin squares. We now do the exact same procedure on each of these new triangles, generating 4 "triangles" of a single square each. In the last step, I simply rewrote these 4 squares in the traditional calligraphy. There's the journey of the hypertrigram.
Figure 3. Calculating Journeys with Triangular Calligraphy.
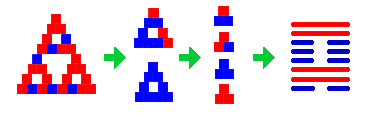
This calligraphy and its associated computation scheme generalize quite easily and painlessly to higher order hypertrigrams, since they are constructed in a recursive manner. Figure 4 illustrates the process for a typical member of TL(3). Notice that although the original TL starts out with a preponderance of yang squares, it becomes highly yin in the next step and eventually evens out to a yin/yang balance by the time we reach the journey figure. This bouncing back and forth is a consequence of the way odd() and fewer() interact in the calculations, tending to "smooth out" differences along the way.
Figure 4. A Typical Third Order Hypertrigram.
A curious consequence of the S(3) symmetries of the journey functions is that if you take any triangle, large or small, within a TL and rotate or flip it any way you want, you wind up with the same journey. You can do multiple rotations and flips of different sub-triangles at any level, including the entire TL, and the journey stays the same. This simply means the journey functions ignore the order of lines in the TL, as we previously noted. It's also interesting to me that there are exactly as many lines in the journey as there are horizontal rows in the high level triangle.
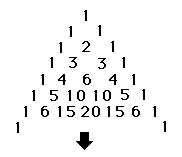As I first studied these new triangular patterns, there was a vague sense of familiarity about them. What suddenly came to me in a flash is their connection with a famous mathematical pattern called Pascal's Triangle, which shows up in many places in mathematics such as probability, combinatorics and even algebra. Pascal's Triangle starts out with the number 1 by itself in the top row, and 1's extending diagonally downward on both sides of the triangle. To compute an entry in the interior of the triangle, you simply add together the 2 entries just diagonally above the new entry, another instance of a recursive definition. For instance, the 5th row has the internal entries of 4 ( = 1+3 from the 4th row) and 6 ( = 3+3 ). I've indicated the first 7 rows completely, hinted at the 8th row, and the arrow at the bottom is a reminder that the triangle extends indefinitely to an infinite number of rows. Now, if you take Pascal's Triangle to a number of rows that is a power of 2 (such as 1, 2, 4, 8, 16, etc.) and color the entries with odd numbers either blue or red, while leaving the even entries blank, you always get a proper hypertrigram! In fact, an n'th order TL (a member of TL(n)) can be painted on the first 2n rows of Pascal's Triangle, and always generates a journey with that same number of lines. Having done an extensive research project on this topic back in college, I was suddenly on very familiar ground. Some of the deeper consequences of this discovery are beyond the scope of this article, however.
In an incredible instance of synchronicity that is common when working with oracular material, I was browsing in a book store 2 days after making this discovery and ran across a fascinating book on the ancient history of mathematics. This book (yes, there actually is a popular book on archeocomputing!), The Crest of the Peacock: The Non-European Roots of Mathematics, by George Gheverghese Joseph, traces the development of important mathematical ideas through many ancient cultures. In quite a number of cases, these old ideas were developed many centuries before their "discovery" by Europeans, a fact conveniently ignored by most modern scholars. I flipped through the chapters on Chinese mathematics, but stopped dead in my tracks when I opened to the page with the drawing at the left. This drawing was reproduced from an ancient Chinese manuscript called the Szu Yuen Chien ("The Precious Mirror of the Four Elements") by Chu Shih Chieh, written in the year 1303 AD. The linear glyphs inside the circles are an old style of writing numbers, called "heng and tsung" rod numerals. Here's a Chinese version of Pascal's Triangle, centuries before Pascal was even born! In fact, this Chinese discovery can be reliably traced back to at least c. 1050 AD. Granted, this is still about 2000 years later than Lao Tse Kaud and the Oracle Temple, but it lends an air of plausibility to the notion that the Wise Ones may have experimented with ideas like this in secret. Needless to say, I was stunned that my modern work on hypertrigrams may actually be very ancient indeed.
As usual, when you develop any new theory, new lines of inquiry seem to open up. Hypertrigrams are no exception. While the presentation in this paper was intended to stay as faithful to the original Q-Ching as possible, it also suggests where the traditional approach made arbitrary, but reasonable design decisions; some of these decisions are open for generalization.
The journey functions developed by the Wise Ones and extended here are extremely wasteful of the total amount of information in hypertrigram, as discussed above in "The Case of the Missing Bits". This is primarily due to the choice of odd() and fewer() to define the interpretation functions, 2 operations that destroy all the order information in a TL. Further, the recursive structures of the TL hierarchy, the journey functions, and the use of only 2 base functions in the definitions, conspire to restrict us to journeys that always have 2n lines. In the traditional trigrams, this means we can only talk about starting and ending hexagrams when the oracle is consulted. In fact, when the trigrams are sons and daughters, there is only one, "non-moving" hexagram generated, even though the wasted information is most abundant in this case. If some of these missing bits could be converted to a new use, it could perhaps allow us to glimpse the "middle" between the beginning and the ending hexagrams. Even more elaborate extensions to the idea of movement could be created, allowing us to fathom the "three ways of standing still" that the Book of Trigrams so mysteriously talks about.
These possibilities could be easily studied by examining other basic functions besides odd() and fewer(). Functions that retrieve some of the order information, such as "which son or daughter is this trigram?", could be especially useful. Only time and experience will tell whether these alternative functions will be as important as the traditional ones. But it only makes sense to shine the reference beams on the hologram from "non-standard" directions, just to see if there are some interesting images hidden there that we are presently ignoring.
In my article on Many Worlds Lines (see McFnordland [2000]), I hinted that MWL lines would be more useful if you could control the probabilities of throwing these lines. Some of these "computer operations" are more useful than others, and it would be helpful to force the yarrow sticks to speak to us in the useful lines more frequently than the weird ones. Ultimately, this could best be accomplished through the usage of "yarrow stick compiliers" that interpret the tosses of the yarrow sticks and transform them into useful "programs" (in the sense of that earlier article). Needless to say, the availability of "wasted information" in the TL hierarchy makes these compilers more feasible. Further research is obviously needed, however.
The journey equivalence classes within TL(n), such as in Table 2, could be easily used to create a topology on the "space" of hypertrigrams. If you interpret each equivalence class as an "open set" of the topology, a rich mathematical structure is imposed on the hierarchy. Such a definition is incredibly easy to create, but that would lead us far beyond the scope of this article. I wanted to mention the idea of "topological spaces of hyper-lines", however, because it is one of the most fertile areas of research in the still emerging field of transfinite lines. If a viable theory of transfinite lines is ever to emerge, I suspect that topological approaches may be one of the best directions for research. Perhaps some practice on these finite spaces of the TL hierarchy will give us some fruitful insights that will carry us over to the infinite regions of the Tao.