An Introduction to Second Order Hyperemblematic Lines
by John McFnordland, Exerr University
(Originally published in Spring 1998 issue of JOAC.)
Abstract: A novel mathematical model of the Hyperemblematic Line hierarchy is developed, with emphasis on the second order lines. The interpretation problem for these nonstandard lines is solved with a recursive algorithm that generalizes the notion of "moving lines" to include the entire "journey" of a hexagram with moving lines over time. Further lines of research are summarized.
The discovery and quick abandonment of hyperemblematic lines by the priests at the Oracle Temple has long been a mystery to historians and a thorn in the side of theoreticians. It is quite evident that the sages made a discovery of incalculable value, but due to the lack of the appropriate mathematical and philosophical tools, they were unable to capitalize on their profound inspiration. It's ironic that now, with the necessary tools readily available to the average college graduate, we can only guess what that original inspiration was. Researchers in recent years have attempted to resurrect this theory of hyperemblematic lines, building on a solid mathematical foundation, but many of these attempts have been less than satisfying. This paper is an attempt to put the field on a firm foundation that can claim to be a follow on to the original spirit of the Q-Ching sages.
The intent of this paper is fourfold. First, the historical and archeological record is sifted to find out what the Oracle Temple priests thought about these nonstandard lines and where they got confused, in order to chart a plausible course for a modern theory. The outlines of this theory, in the language of modern sacred mathematics, is then developed and a framework for handling hyperemblematic lines is laid out, a task the sages apparently could not accomplish on their own. The "interpretation problem" for these lines is then solved via a proposed recursive algorithm that deftly resolves many of the issues that have plagued this field since its inception. Finally, lines of research for the future are sketched out and some of the challenges for future theorists are examined.
(Many of the notions about encoding lines and "n-grams" in a numerical coding, along with the appropriate data compression techniques, that I outlined in a previous article are assumed in the present study. See McFnordland [1995] for details.)
Historical Context for Hyperemblematic Lines
The universe of the Q-Ching is rather limited in scope. The sages had basically two types of lines, the 2 "basic lines" (called yin and yang) and the 4 "emblematic lines" (moving yin, static yang, static yin, moving yang). Lines could be stacked vertically in several ways to form various "n-grams": digrams (2 lines), trigrams (3 lines), and hexagrams (6 lines). While this was a complicated enough system to confuse most initiate programmers for many years at the start of their training, it did have the effect of confining even the greatest of sages to a small world of 10,000 things. Broader vistas would elude them until this basic system could be expanded to include actual infinities.
From this perspective, the discovery of "hyperemblematic lines" (as modern scholars have called them) ranks as one of the most exciting discoveries in the history of divination. Not only were a handful of "new lines" revealed, but more importantly, a recursive technique for expanding the system was created that literally blew it wide open. The Q-Ching universe, for the first time, showed promise of becoming an open ended system.
This entire paradigm shift apparently occured during the days of the famous "Trigram Project" when a student created the hybrid digram shown at the left. Realizing the tight correspondence between "lines" and digrams of lines, it seemed obvious it must represent some kind of new line that didn't fit into the basic or emblematic categories. It was also clear that this digram strained all normal notions of moving and static lines/digrams to the limits of their understanding. They never "made sense" in terms of the traditional numerical encodings, hence seemed to defy interpretation. In fact, the programmers couldn't even agree upon a standard calligraphic representation of these lines in the spirit of straight and broken lines with optional markers for movement, making it more difficult for them to even discourse about the new lines. Other conceptual restrictions also hampered these researches. Ultimately, the blatant disapproval of the emperor's ministers shut down these studies, or rather drove them underground.
The sages did manage to glean a few nuggets of truth from their efforts. One was that the correspondence between digrams and lines was the crucial "Rosetta Stone" for generating and interpretting hyperemblematics. Making a digram out of 2 basic lines creates the 4 emblematic lines, while a hybrid digram of 2 emblematic lines creates the 16 new lines. Digrams are thus a recursive operator for generating new classes of lines from previously known lines. Digrams are also the mechanism for defining the "motions" of a line. The upper portion of a digram determines the initial yin/yang state of the corresponding line, while the negation of the lower part describes the final state. If the two states agreed, the line was termed "static", while if they differed, the line was "moving". While these definitions of movement didn't carry over in a straightforward manner to the hyperemblematics, they still had heuristic appeal as the sages struggled to understand these new objects.
In time, the many roadblocks encountered caused the field of hyperemblematics to be prematurely abandoned. The consignment of these lines to the Bit Bucket is one of the greatest losses for oracular science.
Motivating Intuitions and Common Misconceptions
Unfortunately for modern scholars, that's about as far as the priests at the Oracle Temple got on the topic. Further research was discouraged as being unproductive, although there are hints and rumors that Lao Tse Kaud and other masters made secret attempts to crack the problem. We have very few hints of the proper directions to pursue when developing a theory of hyperemblematic lines. While this gives theorists a wide latitude in what such a theory should look like, it also means no single formulation of the theory (my own included) is likely to gain approval from tradition.
It's important to look closely at first principles, therefore, before jumping off in any particular direction. There are certain foundational issues that will restrict our models, although we may take unconventional interpretations at times when tradition becomes a straight jacket. Further, there are a list of questions and confusions left over from the Trigram Project, particularly the "interpretation problem" for new lines, that a model must address in a satisfying manner. The model must generalize well, allowing for an effortless extension of the Q-Ching universe without resorting to ad hoc principles along the way. And finally, but perhaps most importantly, a model must convincingly reveal the beauty of the Tao. If it doesn't inspire the beholder, it's not likely to be the right path.
There are a number of ground level terms and concepts that are central to this model. Most of them relate to "lines" and "digrams", their respective properties, and how the two concepts are related in the model. In fact, it's impossible to disentangle these two concepts, because "creating a digram" is the recursive technique for creating new lines out of old lines. Since the basic lines (yin and yang) are the starting point of the recursion ("step zero", so to speak), let's begin by examing the lines.
Table 1. Yin and Yang.
| Yin | Yang |
Mother
Dark
Yielding
2 or 0 |
Father
Light
Firm
3 or 1 |
What is a "line" in the Q-Ching? Like the points and lines of Euclidean geometry, an oracular "line" should be considered a primitive or undefined object in the Q-Ching universe. Beyond the facts that lines have a number of "properties" and are subject to certain "operations", we should be willing to be flexible as to how a "line" is imagined, especially when we start creating new lines. In particular, we should not be hung up on traditional geometric or calligraphic conventions for representing lines if the old ways are conceptually restrictive.
The basic lines are characterized by a single property, its (binary) value or "state". In plain English, a basic line is either yin or yang. Please note that these two values have a large number of synonyms or equivalents (see Table 1), and we will likely switch back and forth between these several notations as context dictates. Such frequent "translations" should be of no import to anyone versed in the Q-Ching. Note that some authors have tried to generalize the basic lines to more than two by creating new values beyond yin and yang, usually without much success. We will not treat any non-binary systems in this paper.
Starting with these "basement level" lines, we use the process of "creating digrams" to work our way up to the first floor, the emblematic lines. What is a digram? The traditional, informal definition is "two lines, one on top of another." This description seems a bit overly determined, relying as it does on the common calligraphic representation of figures in the Q-Ching. While it makes sense to say "there's a yin line over a yang line" when describing a digram, the equivalent saying of "there's a 2 over a 3" is not so intuitively obvious. Similarly, calling the component lines in the digram "upper" and "lower" also relies on the overt geometry. Recall also, that the lines in a hexagram are simply numbered 1 to 6 (starting at the bottom); this is known as a "stack" or LIFO (last in, first out) queue. Mathematically, a digram is simply an ordered sequence of lines (in this case, a sequence of length 2), while more generally, an n-gram is an ordered sequence of n lines. And when we say the sequence is "ordered", we simply mean the lines are numbered 1, 2, 3, ... so we know which line follows which. There are any number of equivalent or isomorphic ways of describing such an ordered sequence and we will use any of these notations as the discussion requires.
Digrams introduce a new property, known as "movement". What is movement? Our basic intuition of something that moves is that it's in one place earlier and another place later. In the Q-Ching, "moving lines" don't change their position (by migrating around the hexagram or something), they change their state. Now a (basic) yin line is eternally yin, but a moving yin emblematic line is initially yin, then yang. Yin, as a philosophical concept, is simply yin. But a situation in the world characterized as "moving yin" can only be recognized as moving because of the state change. If you look at the situation only once, no movement is apparent. Similarly, a static yin emblematic line actually means yin now, yin later. It's a subtle, but crucial distinction: basic yin does not equal static yin (emblematic line). Despite the fact that both concepts are represented by the same calligraphic symbol (a broken line), they are not the same. In fact, I would propose an alternative definition of emblematic lines. They do not have two properties of an initial state and an indication of "movement". They do have two properties of initial state and final state. It's this "before and after" picture that gives the impression of static or moving. I explicitly mention this redefinition because it plays a crucial role in our work with higher order lines, particularly when we need to generalize the notion of movement.
Finally, each digram is equivalent to a "line" of some kind or order. This correspondence, equivalence or isomorphism is how new lines are "created". Because digrams and lines are interchangeable like this, we will shift back and forth between these viewpoints with abandon. One of the benefits of this flexibility is the way it solves the "calligraphy problem" or "how do you draw a hyperemblematic line on parchment". The old sages got bogged down by needing to create new graphic symbols for each of the 16 new lines, not to mention the uncounted lines of higher order. By using standard mathematical notation on the equivalent digrams, new lines can be "named" with ease. At least that's one problem that won't be hindering us.
With these prefatory observations guiding our journey, it's time to study hyperemblematics in a more formal manner.
Basic Definitions
In the following rather terse development, we will freely use the ideas and symbolism of modern set theory and computer science to reframe the Theory of Hyperemblematic Lines (commonly abbreviated "HEL"). Some of this machinery, such as functions or ordinal number notation, may be unfamiliar to students of archeocomputing who are not on the theoretical end of the spectrum, so we will start slowly.
A collection of objects is known as a "set". For example, the set of basic lines can be represented in set notation as { yin, yang }. Given the many synonyms for these kinds of lines, this same set could be written as { , }, { 2, 3 } (in traditional numerical symbolism) or even { 0, 1 } (in modern symbolism that recognizes zero). Similarly, the lines in a hexagram can be numbered from 1 to 6, or in modern notation, 0 to 5. The set of line numbers could thus be written { 0, 1, 2, 3, 4, 5 }. In set theory, due to the way integers are defined, a set of the form { 0, 1, ... (n-1) } is equal to the number n -- they literally are the same object.
A "function" is a mapping or correspondence between two sets called the "domain" and the "range". We might write "f : D -> R" to say "f is a function from domain D to range R". By that we mean the function f associates with each item in the set D a unique item in the set R. For instance, any function of the form f : { 1, 2, 3, 4, 5, 6 } -> { yin, yang } will describe a hexagram, since it describes a sequence of 6 yin/yang lines. For any item x in D, the value of the function at x, written f(x), is simply the value in R associated with x by the function f.
Table 2. Plus.
| + | 0 | 1 |
|---|
| 0 | 0 | 1 |
|---|
| 1 | 1 | 0 |
|---|
We will also frequently use a binary operation which we call "plus" and symbolize by a "+" symbol, but it actually resembles the boolean operation XOR. The "addition table" for this operation is given by Table 2. Notice that 0 = 0 + 0 = 1 + 1 -- a number added to itself is always 0. Keep in mind that yin = 0 and yang = 1 -- these are synonyms. For the mathematicians, the set of basic lines with the operation + forms a "group".
Our immediate goal is to define a hierarchy of sets we will call HL(0), HL(1), HL(2), ..., where HL(n) is called the set of hyperemblematic lines of order n.
Def: The "set of basic line states" = BL = { yin, yang } = { 0, 1 } = 2. (Yes, "2"!) Notice that when used in this context of a state, "yin" and "yang" are not capitalized. This is to avoid confusion with the next definition.
Def: A "basic line" is a function f : { 0 } -> BL = { 0, 1 }. There are two such functions, namely Yin (which has Yin(0) = 0) and Yang (where Yang(0) = 1). Yin has any number of synonyms, including 0 and (0), while Yang is sometimes called 1 or (1); these alternatives will make sense shortly. Other synonyms, including the standard broken or straight calligraphic lines, are also frequently used. However, take note of the following notational confusion. Technically speaking, "Yin" (capitalized) is a function equivalent to (0), while "yin" (lowercase) is a single value in the set BL synonymous with 0; similarly for "Yang" and "yang". In common usage, the distinctions between these usages are typically ignored and totally inconsequential, but mathematically, you avoid a lot of messy confusion if you pay attention to this subtle difference.
Def: The set 2N = { 0, 1, ... top }, where the value top = 2N-1 and the value half = 2N-1 (for N >0). Note that 20 = { 0 }, a set with a single item. If it is unclear from context which N is being referred to, the notations top(N) and half(N) may be used.
Def: A "basic hexagram" is a function f : 6 -> BL. (Intuitively, it's an ordered sequence of yin and yang lines of length, or rather height, of 6 lines.) If BL is replaced by the set of emblematic lines, the function is a "hexagram with moving lines". Similarly, if you replace the domain 6 with a domain of 2, you get a digram; a domain of 3 produces a trigram.
Def: An "N-tree" is a function f : 2N -> BL. The intuition is we are forming an ordered sequence or stack of basic lines where the number of lines is a power of 2. The usage of the term "tree" will become obvious shortly. Notice that Yin and Yang are both 0-trees.
Def:If g and h are both N-trees and f is an (N+1)-tree, we say "f is the digram of g and h", written f = ( g, h ), if and only if for all x in the domain of f (that is, x is in the set 2N+1),
f(x) = g(x), if x < half, or
f(x) = h(x-half), if x >= half.
Note that half = half(N+1) in this case, the half-way point in the domain of f. Intuitively, f is a digram of g and h if and only if g determines the lines on the bottom half of the digram and h determines the lines in the top half.
We are now in a position to define the "hyperemblematic hierarchy". As with many such definitions in set theory, this is a recursive definition. In fact, it mirrors the "creating a digram" operation exactly.
Def: The set of "hyperemblematic lines of order n", written HL(n), is defined by:
HL(0) = { Yin, Yang }, and
HL(n+1) = { ( a, b ) : a, b are in HL(n) }.
For those not used to such recursive definitions, they generally have two parts: a starting point (or step zero) and a means of moving from one step to the next. In this case, HL(0) is simply the two basic lines of the Q-Ching, yin and yang. From this, HL(1) is created by looking at all the digrams of basic lines, i.e., HL(1) is the set of emblematic lines. Next, HL(2) is formed by looking at the digrams of lines from HL(1). These are the 16 hyperemblematic lines initially discovered at the Oracle Temple. But why stop there? HL(3) is formed from digrams of HL(2) lines, and so on up to any order of HL(n) you care to create. As is clearly seen, the HL hierarchy is (countably) infinite.
One of the immediate consequences of these definitions is an alternative (and in some ways simpler) characterization of the HL hierarchy.
Thm: For all n, HL(n) equals the set of all n-trees.
Further, by the definition of n-trees, it's possible to calculate exactly how many lines there are in each HL order. For a given value of n, an n-tree has a domain of 2n; for each of these values (from 0 to top), the value of the function can be either 0 or 1, since an n-tree has a range of BL. With 2 choices for each element of the domain, the total number of n-trees = 2 * 2 * ... * 2, where there are 2n factors of 2 in the product. Therefore, the size of HL(n) is exactly 2(2n), establishing the theorem:
Thm: For all n, HL(n) has exactly 2(2n) lines.
This rapid growth in the size of HL(n) was an overwhelming concern for the Oracle Temple staff. HL(0) has 2 lines (yin and yang), HL(1) are the 4 emblematic lines, HL(2) has 16 lines, followed by 256 lines of order 3, 65536 of order 4, 4294967296 of order 5, and then quickly through the roof. Since the old programmers considered infinity to be "the 10,000 things", matters were rapidly getting out of hand, creating a major philosophical crisis. (Integer overflow problems in one's religious worldviews are never considered a good idea...)
As a matter of notation, we will represent an n-tree function as a sequence of 0's and 1's (or any other synonym that's appropriate) within parentheses. For instance, "static yang" is equal to the function f, where f(0)= yin, f(1) = yang (the lower and upper lines of the digram, respectively). As a shorthand, we will denote this line as (yin, yang) or (01) or even (23). The second order line mentioned at the start of this article would be (1111), which is moving yang over moving yang. Alternatively, the usual calligraphic conventions of broken and straight lines in a stack can be used, with f(0) drawn as the bottom line and f(top) as the top line. There are 2n basic lines in the figure for an order n line. In particular, second order lines can be drawn as a stack of 4 lines, sometimes called a "quadrogram" or simply a "quad".
Generalizing the Definition of Moving Lines
The four basic notions of Chinese philosophy are the Tao, yin, yang and "I", which is usually translated as "change". The creation of emblematic lines for oracular use caused the sages to elaborate and extend the ideas of yin and yang. As for "I", the oracle dumbs down a rich philosophical concept to a simple "before and after" state change in the hexagrams. One of the ways of characterizing the "crisis" of HL(2) is that it forces a corresponding change in the concept of change itself within the Q-Ching. There is even room now for cyclic change within the moving lines, which is more in the spirit of "I" than "before and after" ever could aspire to.
As argued earlier, "movement" is not a property of lines in the same way that yin and yang are. Rather, movement is a description of a series of state changes over time. And like the motion of physical objects through space, motion is more than just the starting and final points. There are many distinct paths one can travel to get from point A to point B and each path has its own unique qualities. Similarly, a line that "moves" from yin to yang may make any number of state changes along the way and each history tells a unique story; the effects are even more pronounced when working with full hexagrams. I call the descriptions of these kinds of changes a "journey", since it really relates the entire path a moving line takes, not just the endpoints. I believe the recursive algorithm for journeys developed here is the most satisfactory model of hyperemblematic lines proposed to date.
First a few preliminary, motivating observations. The creation of digrams (and other n-grams) is what allows us to talk about "movement" in the first place. Also notice that digrams and other figures are constructed from the bottom up, but the sequence of states observed is read out from the top down. By that, I mean the upper line is "before", the lower line is "after", when talking about movement, the exact reverse of how the digram is created. You literally start at the top and count down. Finally, for reasons we don't really understand yet, the upper and lower parts of a digram are not treated alike. The initial state is read off the top line directly, while the lower line is negated to give the final state. This negation operation is an inessential part of the way lines are interpretted (a perfectly viable oracular system is left if this operation is dropped), but for historical reasons, it will be retained in this theory. Omitting the negation, which leads to a "rationalized" theory different from the traditional form, actually produces a simpler theory. Many authors will rationalize their theories on the grounds of simplicity ("Occam's razor"), even though it deviates from historical fact in an unimportant detail.
(Just as an aside, it's interesting to speculate what could have happened if the sages had managed to fully develop this "count down" paradigm. After all, the Chinese also invented gunpowder and elementary rocketry, and the evidence at the Oracle Temple shows they were working on computing devices as well. They could have had the major building blocks for a space program, millennia before the Russians and Americans...)
The following presentation is in terms of the general case, i.e., for HL(n), where n is arbitrary. However, for the purposes of giving concrete examples, we will concentrate on HL(2), the second order lines. We start with some preliminary definitions, again.
Def: The function one : D -> BL, where D is some domain (such as 2n), is a function that always has a value of 1, i.e., one(x) = 1 for all x in D. Similarly, the function zero : D -> BL always has the constant value of 0.
Def: Given an n-tree f, not(f) = f + one. That is, for x in the domain of f, not(f)(x) = f(x) + one(x) = f(x) + 1, where "+" is as defined in Table 2. The function "not" essentially causes a line or group of lines to change state, moving from yin to yang or vice versa.
Def: Given an n-tree function f, the "journey n-tree" corresponding to f, written journey(f), is an n-tree function j, such that:
If n = 0, j(0) = f(0), and
if n > 0 and f = (g, h), j = ( journey(not(g)), journey(h) ).
Def: Given an n-tree f, the "state of f at time t", or state(f, t) = journey(f)(top(n) - t). What the factor (top-t) implements is the "count down" technique just mentioned, that is, time proceeds from the top down, not the bottom up. (You could remove this factor by turning the journey n-tree upside down and reading from the bottom up, but this simply has the effect of moving the top-t factor to the definition of journey(f) instead. As will be seen, the current approach simplifies the journey calculations when consulting the oracle.)
The following diagram, Figure 1, illustrates graphically how this computation is carried out for a given second order line. It also demonstrates why these lines are called "n-trees" in the theory, due to their resemblance to the binary tree data structure of computer science.
Figure 1. Computing the Journey of a Line.
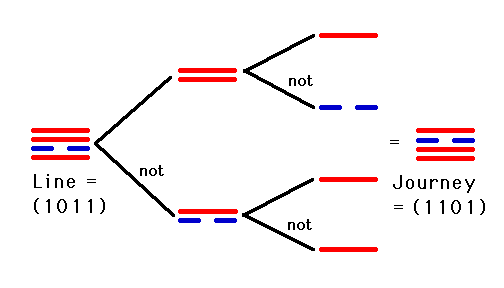
(Please note: to get a "rationalized" form of these definitions, simply replace the recursive step of the the definition of journey(f) by j = ( journey(g), journey(h) ), that is, the "not" is dropped out. Alternatively, not(f) can be redefined to equal f + zero, which is just the same as f.)
While this recursive calculation for the journey of a line "works" for all orders, recursion is a notoriously "high overhead" form of computation. Fortunately, it is possible to isolate all the effects of recursion to a single computation, making it nearly trivial to compute the journey of any line from that point on. It is only necessary to compute the journey for the n-tree zero, which consists of all yin basic lines, from first principles. The following definitions and theorems (which will be stated without the tedious, but quite simple, combinatorial proofs) details this shortcut.
Def: The n-tree "parity" is defined by parity = journey(zero). The name parity is used because of the resemblance of this calculation to the computation of "parity bits" in modern computer memories. In fact, parity(x) will take the value 0 or 1 depending upon whether the number of 1 bits in the binary representation of (top - x) is even or odd. Further note that in a "rationalized" theory, parity equals zero identically.
Thm: For any arbitrary n-tree f, journey(f) = f + parity. In other words, for any value (or line number) x in the domain of f, journey(f)(x) = f(x) + parity(x).
Thm: In a rationalized theory, journey(f) = f. (That's about as simple a calculation as you can get.)
Intuitively, the journey of an n-tree f is derived by flipping certain lines from yin to yang or vice versa. The question of which lines to flip and which to leave alone is determined solely by the parity n-tree, which we calculate once and use in a uniform manner from that point on. Every order of hyperemblematic lines, HL(n), will have a unique parity function. Once a line has been converted to its corresponding journey, the successive states (at time 0, 1, 2, ... top) of the line can be read right out of the journey n-tree, starting at the top and working to the bottom. This algorithm is simple enough that it can be easily taught to anyone capable of mastering the messy yarrow stick method of consulting the oracle. For reference purposes, the mapping from second order lines to their journeys is listed in Table 3. Notice that some of the lines "resemble" the standard 4 emblematic lines. For instance, the second order line (0101) has a journey of (0011), so it is yang for the first half of the journey (steps 0 and 1), and yin the second half (steps 2 and 3). In this sense, it resembles the first order line known as "moving yang" or (11). Similarly, (1001) has a journey of (1111), so it is always yang. This is the same as "static yang" = (01), or even the basic line (order 0) Yang = (1). In general, an (n+1)-tree f is "reducible" to an n-tree g if and only if f = ( not(g), g ). With analogy to the situation in HL(1), f is reducible to "moving g" if and only if f= ( g, g ), although this concept may not mean much for higher order g. Most lines of higher order are not reducible in this sense, because they represent new forms of movement.
Next Page